Compute for pair of pdqr-functions the optimal threshold that separates
distributions they represent. In other words, summ_separation() solves a
binary classification problem with one-dimensional linear classifier: values
not more than some threshold are classified as one class, and more than
threshold - as another. Order of input functions doesn't matter.
summ_separation(f, g, method = "KS", n_grid = 10001)Arguments
| f | A pdqr-function of any type and class. Represents "true" distribution of "negative" values. |
|---|---|
| g | A pdqr-function of any type and class. Represents "true" distribution of "positive" values. |
| method | Separation method. Should be one of "KS" (Kolmogorov-Smirnov),
"GM", "OP", "F1", "MCC" (all four are methods for computing classification
metric in |
| n_grid | Number of grid points to be used during optimization. |
Value
A single number representing optimal separation threshold.
Details
All methods:
Return middle point of nearest support edges in case of non-overlapping or "touching" supports of
fandg.Return the smallest optimal solution in case of several candidates.
Method "KS" computes "x" value at which corresponding p-functions of f and
g achieve supremum of their absolute difference (so input order of f and
g doesn't matter). If input pdqr-functions have the same
type, then result is a point of maximum absolute difference.
If inputs have different types, then absolute difference of p-functions at
the result point can be not the biggest. In that case output represents a
left limit of points at which target supremum is reached (see Examples).
Methods "GM", "OP", "F1", "MCC" compute threshold which maximizes
corresponding classification metric for best suited
classification setup. They evaluate metrics at equidistant grid (with
n_grid elements) for both directions (summ_classmetric(f, g, *) and
summ_classmetric(g, f, *)) and return threshold which results into maximum
of both setups. Note that other summ_classmetric() methods are either
useless here (always return one of the edges) or are equivalent to ones
already present.
See also
summ_roc() for computing ROC curve related summaries.
summ_classmetric() for computing of classification metric for ordered
classification setup.
Other summary functions:
summ_center(),
summ_classmetric(),
summ_distance(),
summ_entropy(),
summ_hdr(),
summ_interval(),
summ_moment(),
summ_order(),
summ_prob_true(),
summ_pval(),
summ_quantile(),
summ_roc(),
summ_spread()
Examples
#> [1] 0summ_separation(d_norm_1, d_unif, method = "OP")
#> [1] 0.3593589
# Mixed types for "KS" method
p_dis <- new_p(1, "discrete")
p_unif <- as_p(punif)
thres <- summ_separation(p_dis, p_unif)
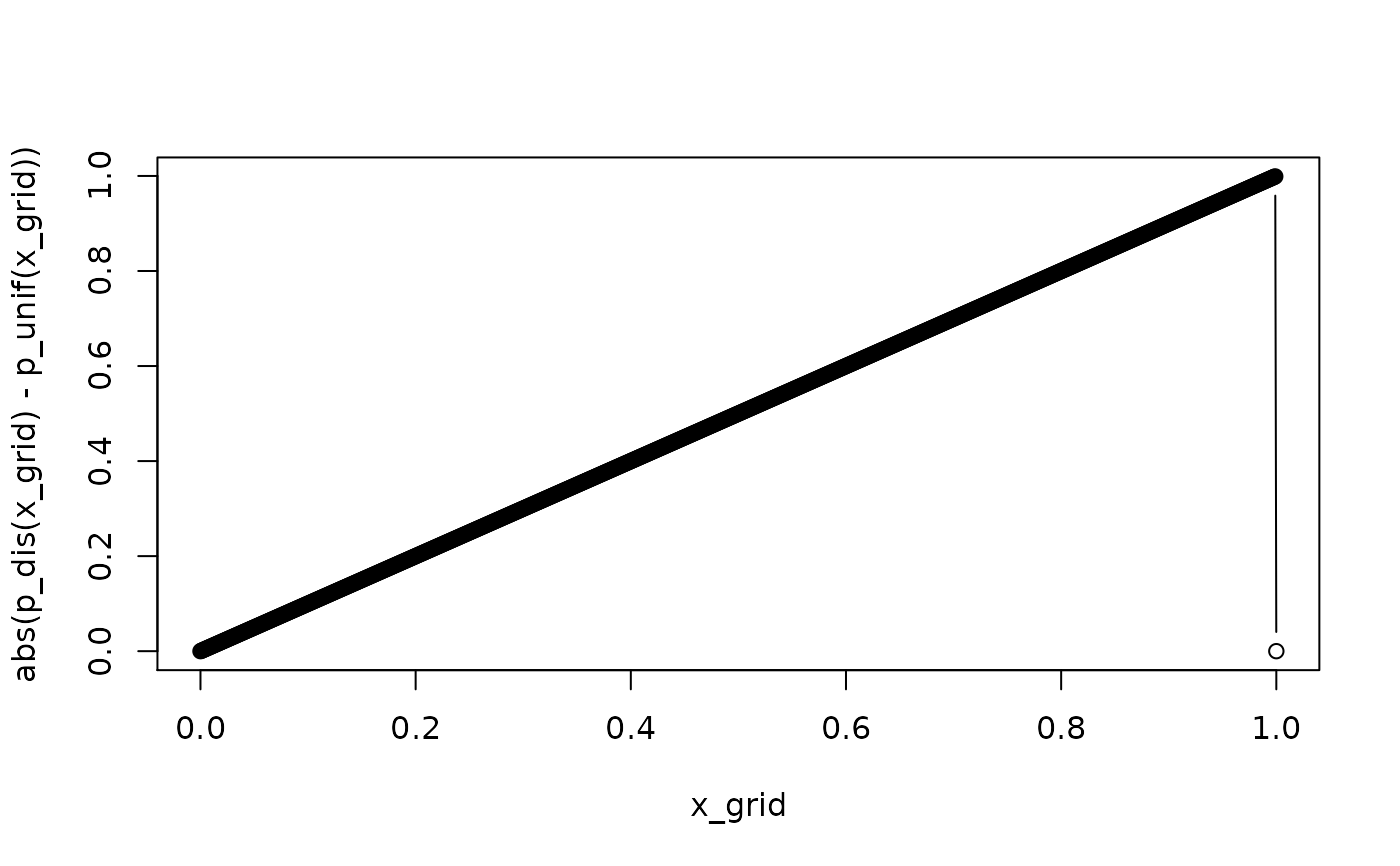
abs(p_dis(thres) - p_unif(thres))
#> [1] 0## Actual difference at `thres` is 0. However, supremum (equal to 1) as
## limit value is # reached there.
x_grid <- seq(0, 1, by = 1e-3)
plot(x_grid, abs(p_dis(x_grid) - p_unif(x_grid)), type = "b")
#> [1] 2.5
# The smallest "x" value is returned in case of several optimal thresholds
summ_separation(d_norm_1, d_norm_1) == meta_support(d_norm_1)[1]
#> [1] TRUE