Based on a list of pdqr-functions and vector of weights form a pdqr-function for corresponding mixture distribution.
form_mix(f_list, weights = NULL)Arguments
| f_list | List of pdqr-functions. Can have different classes and types (see Details). |
|---|---|
| weights | Numeric vector of weights or |
Value
A pdqr-function for mixture distribution of certain type and class (see Details).
Details
Type of output mixture is determined by the following algorithm:
If
f_listconsists only from pdqr-functions of "discrete" type, then output will have "discrete" type.If
f_listhas at least one pdqr-function of type "continuous", then output will have "continuous" type. In this case all "discrete" pdqr-functions inf_listare approximated with corresponding dirac-like "continuous" functions (with form_retype(*, method = "dirac")). Note that this approximation has consequences during computation of comparisons. For example, if original "discrete" functionfis for distribution with one elementx, then probability off >= xbeing true is 1. After retyping to dirac-like function, this probability will be 0.5, because of symmetrical dirac-like approximation. Using a little nudge toxof1e-7magnitude in the correct direction (f >= x - 1e-7in this case) will have expected output.
Class of output mixture is determined by the class of the first element
of f_list. To change output class, use one of as_*() functions to change
class of first element in f_list or class of output.
Note that if output "continuous" pdqr-function for mixture distribution (in theory) should have discontinuous density, it is approximated continuously: discontinuities are represented as intervals in "x_tbl" with extreme slopes (see Examples).
See also
Other form functions:
form_estimate(),
form_regrid(),
form_resupport(),
form_retype(),
form_smooth(),
form_tails(),
form_trans()
Examples
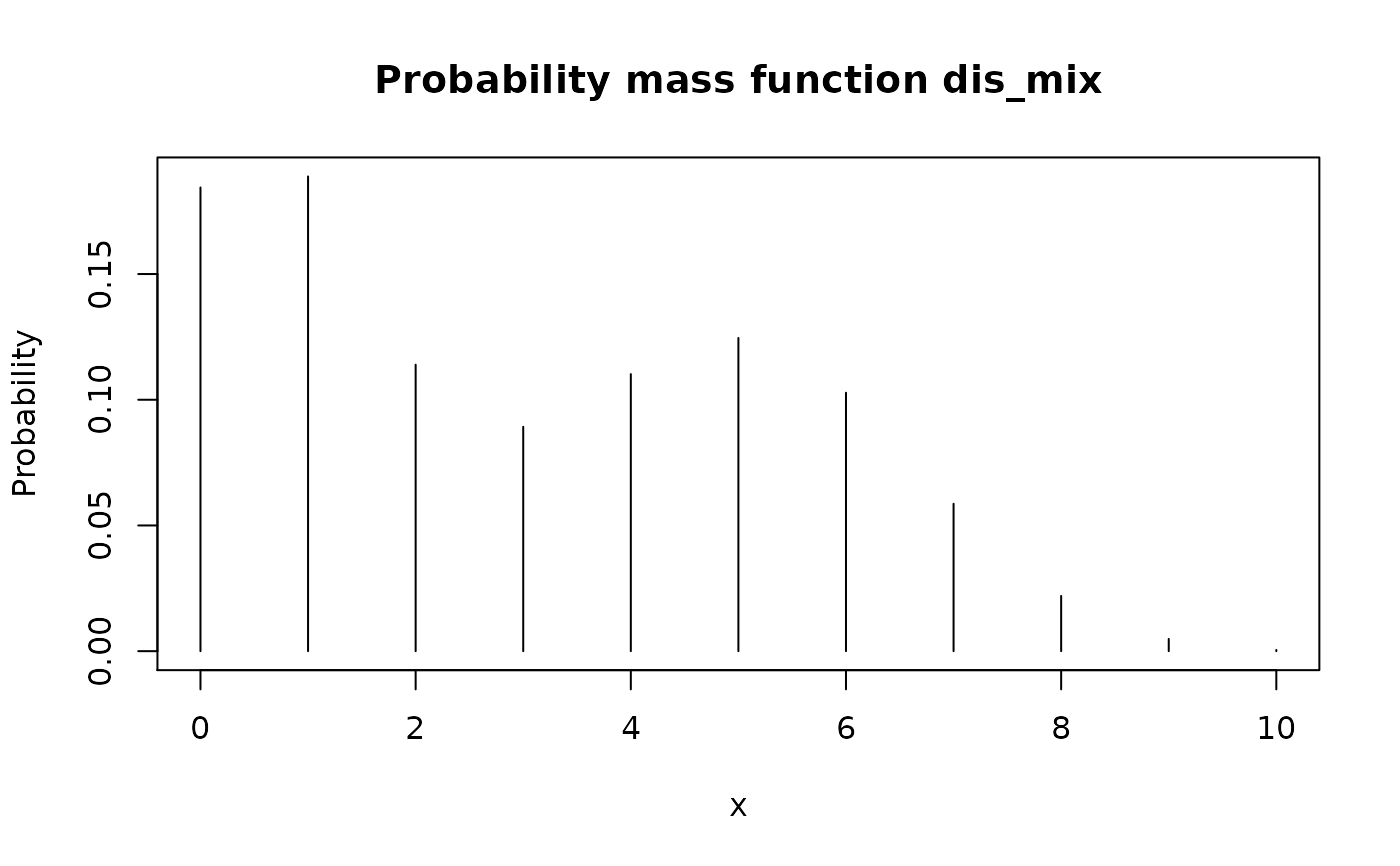
# All "discrete"
d_binom <- as_d(dbinom, size = 10, prob = 0.5)
r_pois <- as_r(rpois, lambda = 1)
dis_mix <- form_mix(list(d_binom, r_pois))
plot(dis_mix)
 # All "continuous"
p_norm <- as_p(pnorm)
d_unif <- as_d(dunif)
con_mix <- form_mix(list(p_norm, d_unif), weights = c(0.7, 0.3))
## Output is a p-function, as is first element of `f_list`
con_mix
#> Cumulative distribution function of continuous type
#> Support: ~[-4.75342, 4.75342] (20005 intervals)
# All "continuous"
p_norm <- as_p(pnorm)
d_unif <- as_d(dunif)
con_mix <- form_mix(list(p_norm, d_unif), weights = c(0.7, 0.3))
## Output is a p-function, as is first element of `f_list`
con_mix
#> Cumulative distribution function of continuous type
#> Support: ~[-4.75342, 4.75342] (20005 intervals)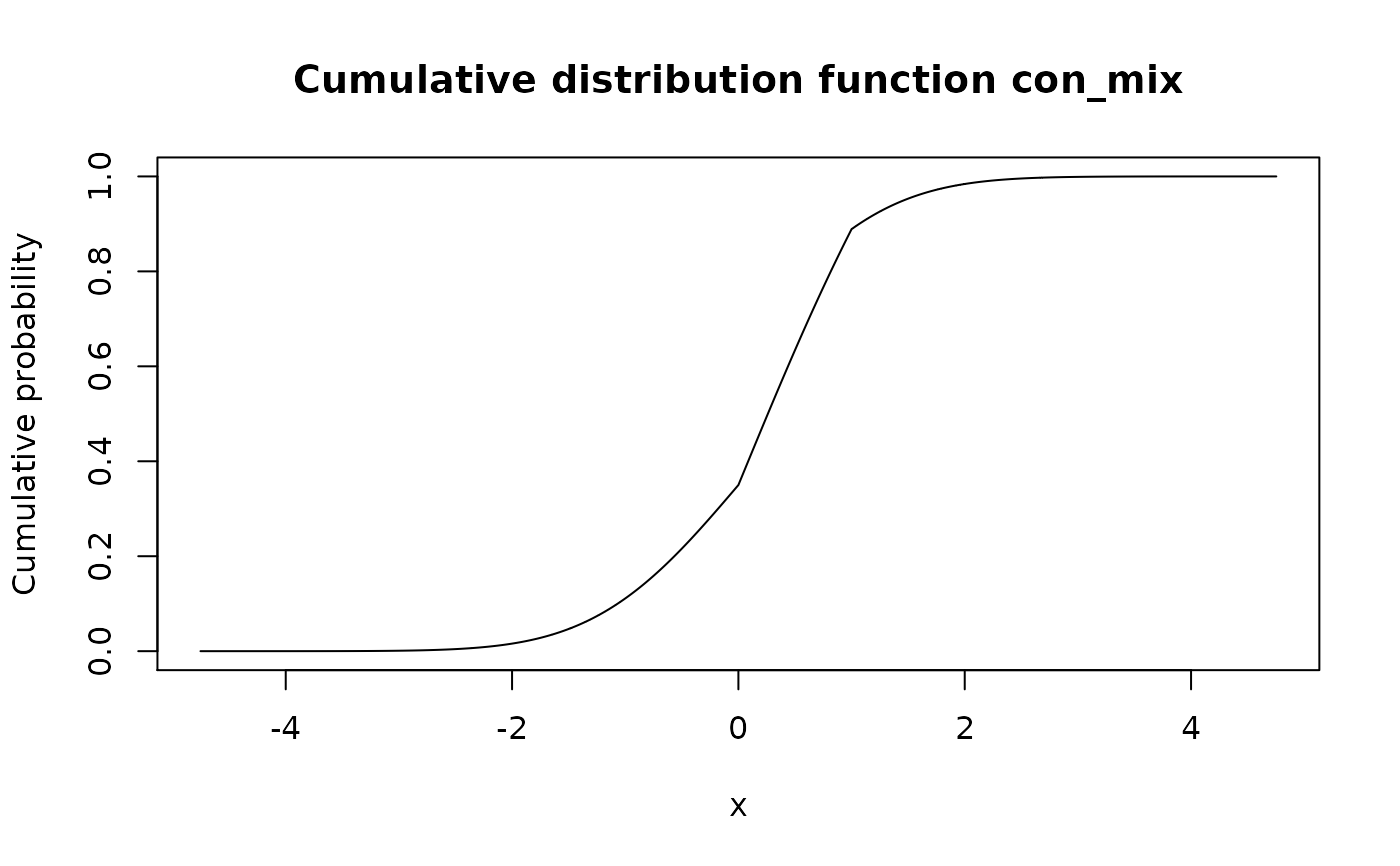 ## Use `as_*()` functions to change class
d_con_mix <- as_d(con_mix)
## Theoretical output density should be discontinuous, but here it is
## approximated with continuous function
con_x_tbl <- meta_x_tbl(con_mix)
con_x_tbl[(con_x_tbl$x >= -1e-4) & (con_x_tbl$x <= 1e-4), ]
#> x y cumprob
#> 5001 -1.000000e-08 0.2792602 0.3500000
#> 5002 -2.904343e-12 0.4292166 0.3500000
#> 5003 0.000000e+00 0.4292602 0.3500000
#> 5004 1.000000e-08 0.5792602 0.3500000
#> 5005 1.000000e-04 0.5792601 0.3500579
## Use `as_*()` functions to change class
d_con_mix <- as_d(con_mix)
## Theoretical output density should be discontinuous, but here it is
## approximated with continuous function
con_x_tbl <- meta_x_tbl(con_mix)
con_x_tbl[(con_x_tbl$x >= -1e-4) & (con_x_tbl$x <= 1e-4), ]
#> x y cumprob
#> 5001 -1.000000e-08 0.2792602 0.3500000
#> 5002 -2.904343e-12 0.4292166 0.3500000
#> 5003 0.000000e+00 0.4292602 0.3500000
#> 5004 1.000000e-08 0.5792602 0.3500000
#> 5005 1.000000e-04 0.5792601 0.3500579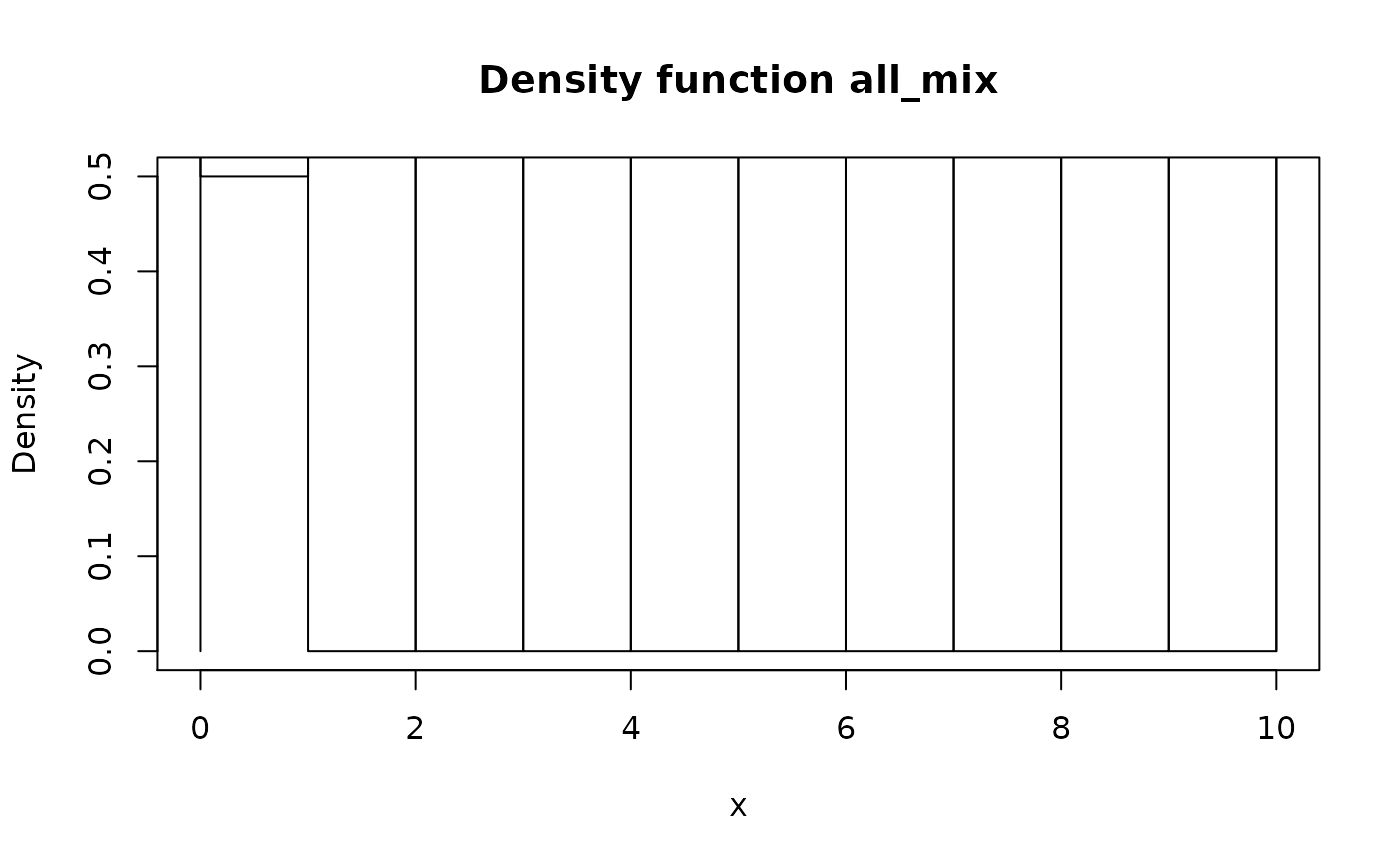 all_x_tbl <- meta_x_tbl(all_mix)
## What dirac-like approximation looks like
all_x_tbl[(all_x_tbl$x >= 1.5) & (all_x_tbl$x <= 2.5), ]
#> x y cumprob
#> 10006 2 0 0.5053711
#> 10007 2 2197266 0.5163574
#> 10008 2 0 0.5273437
all_x_tbl <- meta_x_tbl(all_mix)
## What dirac-like approximation looks like
all_x_tbl[(all_x_tbl$x >= 1.5) & (all_x_tbl$x <= 2.5), ]
#> x y cumprob
#> 10006 2 0 0.5053711
#> 10007 2 2197266 0.5163574
#> 10008 2 0 0.5273437